New PID-algorithm for automated glucose clamps

Introduction

The euglycemic, hyperinsulinemic glucose clamp is the gold standard for the determination of pharmacokinetic and pharmacodynamic (PK/PD) effects of new anti-diabetic drugs, in particular insulins. In a typical glucose clamp experiment, a drug-induced decline in blood glucose (BG) concentrations is prevented by infusing glucose at a variable rate, so that BG is "clamped" at a pre-determined target level.

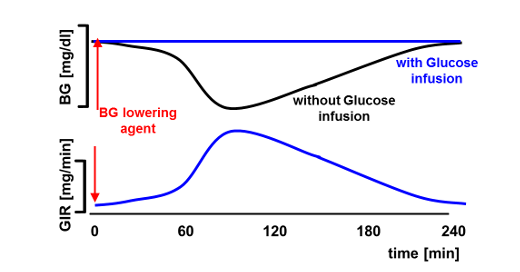
In automated glucose clamps the glucose infusion rate (GIR) which is needed to keep the BG as close as possible to the target level is calculated automatically by a pre-programmed algorithm. The first automated glucose clamp device was the Biostator with an in-built algorithm for calculating GIRs [1]. Although the Biostator was used in thousands of glucose clamp experiments, the algorithm has some limitations:

The Biostator algorithm was designed in the 1970ies when fast and ultra-fast acting insulin analogues were not yet available. The algorithm therefore reacts too slowly to compensate for the fast onset of action of these insulins.

The Biostator algorithm does not separate the proportional and the derivative part of the control algorithm which makes it difficult to optimize the algorithm for different settings and different insulins.

We therefore decided to develop a new clamp algorithm for rapid-acting insulins based on the PID controller approach. The new algorithm could be implemented in modern glucose clamp devices such as ClampArt. Clamp quality parameters [2] were compared between the Biostator algorithm and the new Clamp-PID algorithm.

Methods

In-silico development

The following PID-approach was used for the new Clamp-PID algorithm:

GIR = k_p * f_p  +  k_i * f_i  +  k_d * f_d

with

f_p = (BG – target level),    f_i = mean GIR,    f_d = slope of BG-values

and unknown coefficients k_p, k_i, k_d.

The first step was an in-silico optimization of the unknown coefficients by numerical simulations. The numerical glucose clamp simulator uses a single compartment description of glucose kinetics with an exponential absorption of insulin from the subcutaneous tissue and exponential insulin clearance from plasma. The new BG concentration is calculated from the previous BG concentration by using a log-normal profile for a fast acting insulin action for lowering BG and the Clamp-PID algorithm for calculating the glucose infusion rate for increasing BG. Additionally, sensor noise was added to the BG values using normally distributed random values reflecting the measurement error of the glucose sensor.

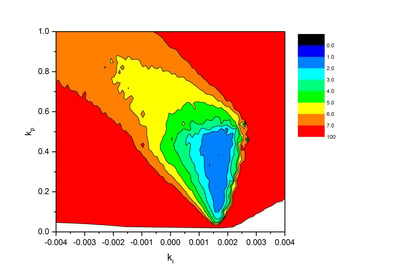
The coefficients k_p and k_i for the proportional and the integral part of the control algorithm were optimized in 1600 glucose clamp simulations with a rapid acting insulin profile to reduce fluctuations in BG and thereby increase precision. The figure shows a systematic approach with different combinations of both parameters to find the best set of coefficients. For each combination glucose clamps were simulated and the resulting clamp quality parameter “precision” is color-coded in the figure.

In-vitro verification

In a second step the best set of coefficients was tested in in-vitro experiments with the original ClampArt device using the original tubing set: A double lumen catheter was used to pump the glucose solution out of a 5 L container to the ClampArt glucose sensor and an infusion tubing set was subsequently used to ”infuse” glucose solution via the ClampArt glucose infusion pump into the container. The insulin induced glucose lowering effect was simulated in the container by diluting the glucose solution with water infused at variable rates by a computer-controlled pump. The glucose clamp quality parameters [2] precision (standard deviation of all BG values) and absolute control deviation (mean of absolute differences between target level and BG values) were compared between both algorithms. 

Results

The following figures show two individual in-vitro glucose clamp experiments with either algorithm.

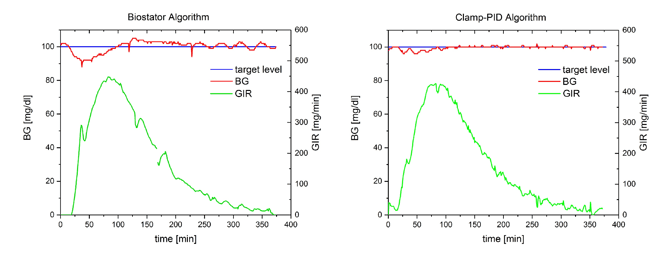
The Biostator algorithm shows a dip in BG values of about 10 mg/dl at the beginning of the insulin effect and the BG values are above target for about 2 h after the maximum insulin effect. In comparison, the deviation of BG curves from BG target are considerably smaller with the Clamp-PID algorithm translating into improved values for the clamp quality parameters precision and control deviation, shown in the following table.

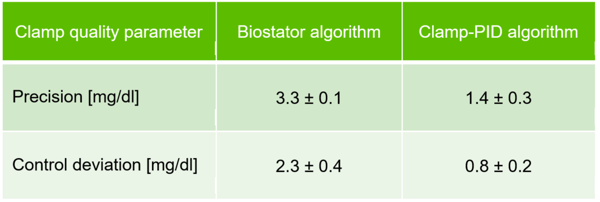
In the small in-vitro study precision is improved more than twofold whereas control deviation increased almost threefold.

Conclusion and outlook

The new Clamp-PID algorithm leads to faster reaction to insulin-induced changes in glucose infusion rates. This lowers deviations (over-/undershooting) in BG as required by regulatory guidelines for physiological closed loop controllers, e.g. IEC 60601-1-10 [3].

The new Clamp-PID algorithm substantially improved glucose clamp quality in in-vitro experiments with regard to precision and control deviation.

The new Clamp-PID algorithm is now investigated in a clinical glucose clamp study.